VecTcl

Linear regression benchmark

Release .zip Release .tar.gz Other versions

Linear regression benchmark

Given 2 Tcl lists with doubles x and y, compute the linear regression line $y\approx \alpha+\beta x$ . VecTcl is the clear winner in this contest (apart from C, which is included as the baseline):

Linear regression, computation only Linear regression, setup included

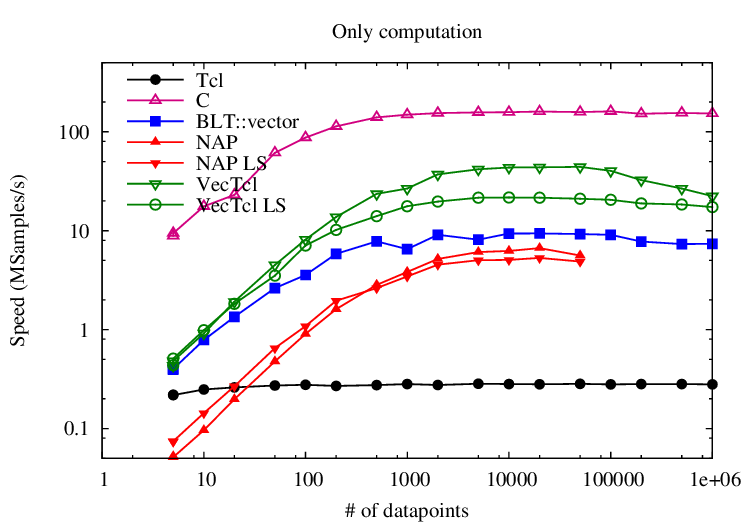
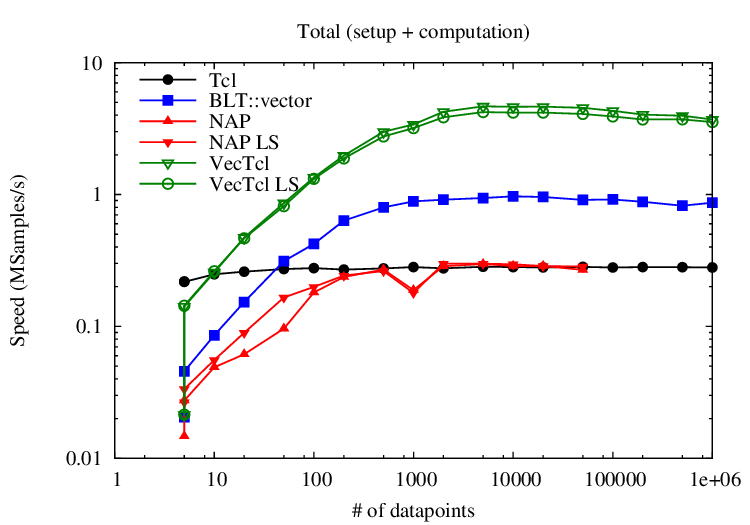
The first image shows the performance (measured in number of datapoints processed per second) for the computation only; the second includes also the time of converting from Tcl lists to the internal data structure. VecTcl is the clear winner in this contest, both for the computation itself as for the conversion of the data. The code in VecTcl looks like this:

vexpr { 
	xm=mean(xv); ym=mean(yv)
	beta=sum((xv-xm).*(yv-ym))./sum((xv-xm).^2)
	alpha=ym-beta*xm
}

Compared to the C solution, there is still a large gap to bridge. At small numbers of datapoints, the time is completely dominated by the one-time costs. The C solution comprises only 1 function call numarray::linreg, whereas the VecTcl solution compiles into 12 nested function calls. For large number of datapoints, the speed is limited by the memory bandwidth. The C solution needs only 2 passes over the dataset, whereas the VecTcl solution does 4.5 - hence a slowdown of 2.5 is reached between 5000 and 20000 datapoints. For even larger numbers (>20000), VecTcl becomes slower again, as soon as the temporaries exceed the cache.

This is the inner loop in C:

int i;
double xm=0.0; double ym=0.0;
for (i=0; i<length; i++) {
	xm+=x[i*xpitch]; 
	ym+=y[i*ypitch];
}
xm /= length;
ym /= length;

double xsum = 0.0; double ysum = 0.0;
for (i=0; i<length; i++) {
	double dx=x[i*xpitch]-xm; 
	double dy=y[i*ypitch]-ym;
	xsum += dx*dy;
	ysum += dx*dx;
}

double b = xsum / ysum;
double a = ym - b*xm;

And here comes the math:

There are two possible ways to complete this task.

Using the direct formula

$$ \begin{align} \bar x &= \frac{1}{N} \sum x_i\\ \bar y &= \frac{1}{N} \sum y_i\\ \beta &= \frac{\sum_i(x_i-\bar x)\cdot(y_i-\bar y)}{\sum_i (x_i-\bar x).^2}\\ \alpha &= \bar y-\beta\bar x \end{align} $$

Computing the least-squares solution to the system

$$ \begin{align} A p &= y\\ A &= \begin{pmatrix} 1 & x_1\\ 1 & x_2\\ \vdots & \vdots\\ 1 & x_N \end{pmatrix}\\ p&=\begin{pmatrix} \alpha & \beta \end{pmatrix} \end{align} $$

Only “VecTcl LS” and “NAP LS” use the matrix decomposition, the other solutions compute the direct formula.